안녕하세요! 데코입니다!
오늘은 네이버 '사다리 게임'의 확률이 일정한지 실험하고 확인해 보는 포스팅을 하려고 합니다!

1. 분석 계기

네이버에 '사다리게임'을 검색하면 간단하게 게임을 만들 수 있다는 것 아시나요?
분석팀에서 종종 점심 먹으러 갈 때 미리 식당에 가서 음식을 주문하는 선발대를 1명 뽑아서 가요!
제가 최근에 네이버 사다리 게임을 통해서 선발대를 뽑는 게임을 만들었는데!
팀장님이 연속 4번 선발대로 뽑히는 일이 발생했어요...!
그래서 과연 네이버 사다리 게임 확률이 일정할지(=기댓값 동일한지) 확인해 보는 포스팅을 해봅니다!
2. 가설 설정
가설은 아래와 같이 세워보았어요!
귀무가설: 사다리 게임에서 선발대 당첨 기댓값은 '(실험 횟수/참여 연구원 수)'로 동일할 것이다.
대립가설: 사다리 게임에서 선발대 당첨 기댓값은 동일하지 않을 아니다.
3. 실험 횟수 설정
네이버 사다리 게임에서 몇 회의 실험을 할지는 중심 극한 정리를 활용해서 '60'으로 결정했어요!
중심극한 정리(CLT, Central Limit Theorem)란, 독립적인 확률 변수들의 평균이나 합이 어떤 분포를 따르더라도, 해당 분포와 무관하게 표본의 크기가 충분히 크다면, 이들의 평균이 근사적으로 정규 분포를 따르게 된다는 정리입니다.
이때 표본의 크기가 얼마나 충분한지는, 해당 모집단의 분포에 따라 달라지며, 일반적으로는 최소 30개 이상의 표본이 있다면 충분하다고 여겨집니다.
사다리 게임에서 발생하는 분포는 대략적으로 대칭적이고 분산이 적을 것으로 예상이 되니까!
최소 표본인 30에 2배인 60회 실행했어요!
4. 데이터 수집(획득)
Python에 Selenium을 이용해서 xpath와 click()을 이용해서 60회만큼 자동으로 실행할 수 있을 것 같은데...!
지금은 수가 적으니까 60회를 일일이 클릭해서 결과를 csv로 저장했어요!
(나중에 시간이 되면 데이터도 자동으로 획득하는 코드를 작성해 볼게요!)

사다리 게임에서 아래처럼 A~F 6명을 입력하고, 1명의 선발대 그리고 5개의 후발대로 설정했어요!


60회 모두 동일한 환경으로 반복해서 데이터를 얻었습니다!
이렇게 나온 사다리 결과를 csv 파일로 저장했어요!
확률이 동일하다고 하면 A~F 모두 10번씩 선발대에 당첨이 될 것이라고 생각이 드네요!
(물론 오차는 존재하겠지만요!)

5. 가설검정
가설 검정을 위해 카이제곱 검정을 이용했어요!
카이제곱 검정은 예상값과 실제 관찰값의 차이가 통계적으로 유의한 지를 검증하는 방법 중 하나예요!
60번의 사다리 게임에서 기댓값은 60 / 6 = 10
실제 관찰값인 선발대 당첨수는 사다리게임실험.csv에 의하면 A~F 각각 (8, 13, 9, 8, 9, 13)이에요!
이걸 분할표로 만들어보았어요!
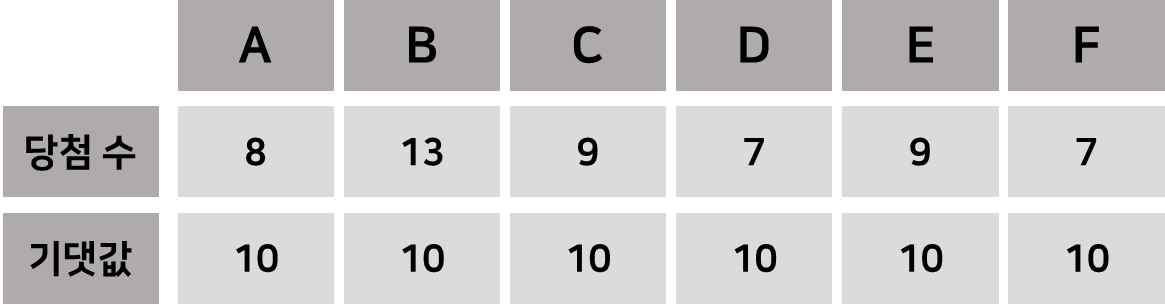
그다음에 python을 이용해서 가설 검정을 진행했어요!
scipy 패키지의 stats 모듈에서 제공되는 chi2_contingency 함수를 사용하여 수행했습니다!

오...! p-value가 엄청 크게 나왔네요!
유의 수준 0.05에서 귀무가설을 기각하지 않고 채택하는 결과를 알 수 있습니다!
결론 : 귀무가설을 채택한다!!!
(귀무가설: 사다리 게임에서 선발대 당첨 기댓값은 '(실험 횟수/참여 연구원 수)'로 동일할 것이다.)
실험을 통해 네이버 사다리 게임에서 선발대 걸릴 확률은 동일하다는 것을 확인했어요!
네이버 사다리 게임에서 선발대를 뽑는 게임을 실행했었기 때문에
네이버 사다리에서 직접 실험을 60회 실행해서 선발대 걸릴 확률은 동일하다는 것을 확인해 보았어요!
선발대에 당첨 확률은 1/6으로 약 0.166이니까
팀장님이 연속 4번 걸리셨던 것은 (1/6)^4 = 0.00077 (약 0.077%)의 값으로 엄청난 우연이였네요!
앞으로 점심시간 선발대 정할 때 사다리 게임 계속 이용하겠습니다...!
설명이 어려운 부분 혹은 잘 이해가 안 가는 부분
그리고 더 궁금한 내용이 있다면
언제든지 댓글로 남겨주세요!
빠르게 궁금증을 해결해 드릴게요!
공감과 댓글은 큰 힘이 됩니다!
오늘도 블로그 방문해 주시고
포스팅 읽어주셔서 감사합니다!

'Data Science > 일상 속 분석' 카테고리의 다른 글
| [일상 속 분석] 데이터 분석가 채용에서 요구하는 능력은 무엇일까?(워드클라우드 사이트 추천!) (38) | 2023.04.02 |
|---|
